Call for retraction of paper entitled: "Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission"
Authors: David N. Fisman, Afia Amoako and Ashleigh R. Tuite
Update: TRISH WOOD’S interview with Denis Rancourt and Byram Bridle.
And also: look for my comment listed here and check out Denis Rancourt’s response below.
First of all, please refer to this thorough and excellent review of the paper by Byram Bridle, and a list of scientific reasons why the aforementioned paper should never have been published. This paper indeed went through peer review. Who were the reviewers? I smell an investigation coming your way.
My take? The point of publishing a low level piece of writing like this is to create division. It is that simple. There is no scientific merit in this piece (I will demonstrate this) and the message is not science-based: the message is that the ‘unvaccinated’ need to be ‘vaccinated’.
Risk among unvaccinated people cannot be considered self-regarding, and considerations around equity and justice for people who do choose to be vaccinated, as well as those who choose not to be, need to be considered in the formulation of vaccination policy.
You know what that means? It is difficult to read between the lines of their contrived bullshit to discern meaning here, yes, but basically they are saying “Screw you and your body autonomy. You don’t deserve rights for choosing what you chose and this should actually be written into law.”
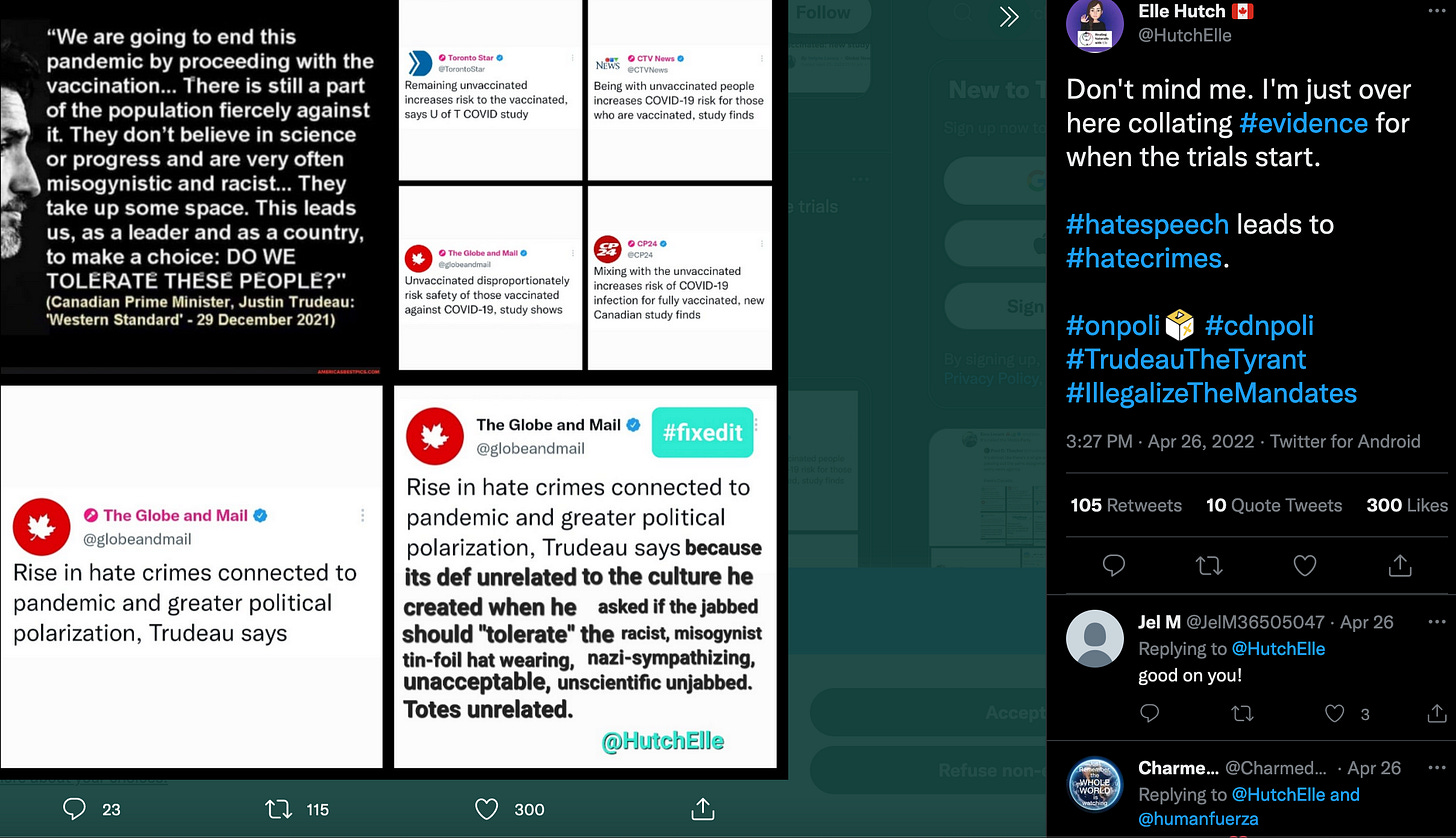
A Canadian mother and researcher has been documenting the use of this kind of misinformation to collate the usages on the ‘Twitter’ platform and specifically, how the use of such language from our ‘leader’ as ‘DO WE TOLERATE THESE PEOPLE’, in reference to the people who have chosen not to be injected with the experimental COVID-19 products, can lead to division, hate and chaos. This is the goal.
There are 13 legacy media outlets reiterating the misinformation in this article as of April 25, 2022.
Now onto the ‘paper’. It is entitled:' “Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission”1 and was penned by David Fisman, who has served on advisory boards for Pfizer and AstraZeneca, and Ashleigh Tuite who was employed by the Public Health Agency of Canada when the research was conducted. The other author Afia Amoako is a student. They claim all authors contributed equally.
I won’t deconstruct this paper as thoroughly as Byram did, but since I have a degree in Applied Mathematics, I will approach my criticism from this particular vantage point.
As part of the Applied Mathematics program, we were taught how to build systems of (differential) equations using the (Kermack and MacKendrick) Susceptible, Infective and Removed (SIR) model as an example model system, as it is useful for modeling viral dynamics and epidemics. It is useful in that an assumption that the rate of transmission of a microparasitic disease is proportional to the rate of encounter of susceptible and infective individuals, modelled by the proportion, is made. The SIR model is 3-dimensions (utilizes 3 variables: S, I and R) and is simplistically elegant. The textbook I used the most was Mathematical Models in Biology by Leah Edelstein-Keshet2, if you’re interested.

The reason I mention this is to drive home the fact that I know SIR models. They were the foundation of my own models that I built for my Master’s and my PhD works. This very simple system of 3 equations has been used countless times throughout the years to gain insights into viral dynamics and epidemics. For example, in a paper published in Science, a simple 3-equation ODE model was used to elucidate that during the chronic phase of HIV infection, the estimated HIV-1 production rate was much higher than previously assumed.
Back to the paper. The claim in their paper is that they explored respiratory infectious disease dynamics of 2 mixed populations using “a simple compartmental model of a respiratory viral disease”.
People are represented as residing in 3 possible “compartments:” susceptible to infection (S), infected and infectious (I), and recovered from infection with immunity (R). We divided the compartments to reflect 2 connected subpopulations: vaccinated and unvaccinated people.
What they describe as the basis of their constructed model is the SIR model.
Below is the screenshot (top right) of the model that they refer the reader to as the ‘simple’ model that they constructed. It is 15 equations and has many more parameters. Simple?
Now, the very first thing a good professor will tell a student about learning to mathematically model a dynamical system is to keep things simple. Minimize the number of variables and parameters. The more contrived and convoluted a system of equations gets, the less meaning it will ultimately have. The increase in the number of variables tends to ironically decrease the degree of ‘reliability’ with regard to mimicking the real system, and it is always prudent to keep the number of parameters required to be estimated as low as possible since estimating parameters can be very difficult and the more ‘estimates’ input, the less reliable the model output may become.
These are the basics in modeling.
There is an ongoing dispute between biologists and mathematicians about the value of mathematical models as being able to reasonably predict anything in biology. I understand the concern, but I also understand the value of modeling. If a mathematical model is built from non-biased assumptions based in biology, has a minimal number of variables (and parameters), and has undergone many rounds of careful criticism, it can be extremely valuable in its predictive ability.
That system of equations as published in the Appendix (https://www.cmaj.ca/content/cmaj/suppl/2020/04/08/cmaj.200476.DC1/200476-res-1-at.pdf), as shown below in a blown-up screenshot, would be the quintessential example of what NOT to do when building a good model with potential predictive quality. It’s ridiculous, in my opinion. I actually remember during my degree program that there was an example model system of 16 equations that was used as the example of an unreliable model. I would NEVER look twice at their model. I don’t care what it is meant to be modeling or predicting. I wouldn’t consider it as a useful tool.
My goal in writing this piece is not to pick on their model, per se, but to reinforce that I am trained in this type of modeling and from my point of view, this model they use is one I would approach with severe caution with regard to drawing conclusions. There are too many variables and there are too many parameters. How did they estimate these parameters and where are the confirmations of these estimates? Did they calculate them based on data? Did they approximate them from models? Did they make them up to fit their conclusion?3 And no, I am not kidding. This happens.
Perhaps the most important point I would like to make is this: if one single parameter value is altered, the entire result of the model changes in turn.
As part of a good Applied Math degree program, one will be introduced to something called bifurcation analysis or theory. The only thing the reader needs to understand about this is that in dynamical systems (systems that change in time), there can be parameters that are more ‘sensitive’ than others. For example, if you change one of these sensitive parameters, the entire dynamical behaviour of the system may change. What this indicates is that you have discovered a bifurcation point where there is a shift in qualitative behaviour of a system based on a quantitative change. The existence and stability properties of equilibrium points are affected by these parameters. They did not do a bifurcation analysis and I will not do one either.
The reason I mention this is to drive home the relevance of ‘accurate’ parameter estimation in modeling. Two different values could yield two completely different system behaviours. Let’s return to the paper for the perfect example of this.
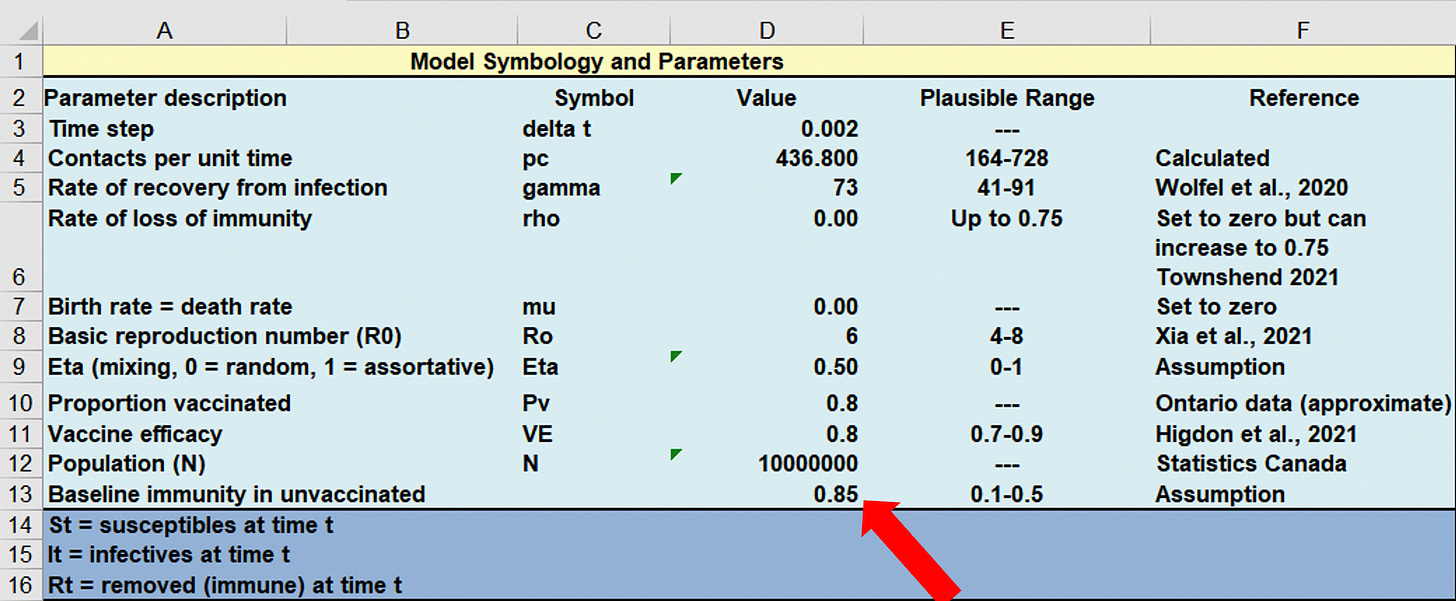
The authors allow the reader to use their data and model to verify their findings. This is great, by the way, and in my experience, not common. But… Take a look at the following table where the red arrow points to 0.2. This is the percentage of people assumed by the authors to be immune in the ‘unvaccinated’ population. Notice also, there is no reference for this. They simply write ‘Assumption’ in the ‘Reference’ column. Remember what I wrote about making up parameter values? It happens.
So, by the author’s assessment, the default value used for baseline immunity among the ‘unvaccinated’ population was 20%. A peer-reviewed published scientific paper suggesting that ~90% have immunity can be read here. So it is unclear to me why, since this is published, the authors did not use this 0.9 value as they would have avoided their ‘Assumption’ and would have a referenced citation.
Their model system’s behaviour is based on ‘Model outputs - contribution to risk among vaccinated from unvaccinated’ as an output of the model, according to the authors. In the far right column, the reader can see that the output ‘Ratio of fraction of infections acquired from unvaccinated to fraction of contacts unvaccinated’ under the purple arrow. The values under the purple arrow indicate that transmission is occurring disproportionately from ‘unvaccinated’ people to ‘vaccinated’ people. Remember this.
Let’s do an experiment. Let’s change the value of the ‘Assumed’ parameter of 0.2 to 0.9 and see what happens to the system’s behaviour with regard to the output. You know what, let’s go easy and use 0.85. This means, again, that 85% of people have naturally acquired immunity in the ‘unvaccinated’ population.
As shown in the following table, transmission is occurring disproportionately from ‘vaccinated’ people as indicated by the ratios less than 1! What this means in actuality is that the ‘unvaccinated’ are serving as a buffer for the ‘vaccinated’ - exactly what we have been saying the child populations have been doing this entire time. Well, except the injected children.
The conclusions of the paper are reversed by changing the value of a single parameter.
This isn’t even the most disturbing aspect to me. What disturbs me the most is that this parameter value was assumed, and the assumed value was at the opposite end of the spectrum as the peer-reviewed assessed value reported here - an actual value - not an assumed value to fit the data. This is the biggest NO-NO you can perpetrate in modeling!! You could get kicked out of university for this and would most certainly fail your modeling course.
This is a prime example of what not to do with regard to modeling, in my opinion. This paper should not have been published and since it has been, it should be retracted.
My email:
https://www.cmaj.ca/content/cmaj/194/16/E573.full.pdf
https://archive.org/details/mathematicalmode1988edel
https://www.cmaj.ca/content/cmaj/suppl/2020/04/08/cmaj.200476.DC1/200476-res-1-at.pdf












Thank you for this post. My medical school gave us ZERO guidance on dissecting journal articles and discovering potential pitfalls. Everything I learned about evaluating scientific evidence was in surgery residency and it was spotty at that, wholly inadequate for determining which evidence should influence my practice, which now looks like it is designed to be that way. We are encouraged to "follow the guidelines," but who watches the watchers? Obviously our peer review system is not doing its job.
Dr. Rose, this is beautifully written as usual and made a complex topic understandable. Keep up the great work!
J. Hogan, MD
Thank you Jessica and also Byram Bridle for calling this one out!
My mental health plummeted just the other day when I was first made aware of this "study". I don't actually want to call it a study either, because it's essentially just a mental game they played with imaginary values plucked out of thin air, from what I can tell.
I saw the hostile nature and the division it was intended to cause. And see the general apathy of those who don't understand. The typical vaccinated citizen.
I feared an imminent witch hunt and felt like I needed to head for the hills or set plans for it. I made a bug out bag. Better safe than sorry.
I have calmed down a bit now. Thank you. Seriously.