The Achs DNA paper launched in an attempt to debunk the truth, is debunkable
The “plasmid equivalents” approach is bad...
Addendum: Throwing in some Lander-Waterman framework on Kevin’s suggestion to check it out. It’s used for shotgun sequencing coverage to get an idea of the expected fraction of a target genome (in this case it’s the ~7,824 bp plasmid template), covered by random reads/fragments. It also outputs redundancy which tells you how many times a base is covered by overlapping fragments: a high number means the sequence is pieced together well from many overlapping bits: good for coverage; not so good for “plasmid equivalents”.
Here’s how it works:
Expected coverage fraction = 1 - e^{-c}where c (redundancy)
= (total bases sequenced / plasmid length)
= (N × L) / G
N = number of reads/fragments
L = average read/fragment length
G = genome/plasmid length (~7,824 bp).
So an estimate of total fragments from qPCR - the KAN target (backbone region) represents ~63 / 7,824 ≈ 1/124 of the plasmid as shown before (or below). Assuming uniform random fragmentation (DNase digestion approximates this), detected KAN-bearing fragments ≈ total plasmid-derived fragments / 124. Therefore, the estimated total fragments is N ≈ 9.8 × 10^8 × 124 ≈ 1.22 × 10^11, per dose.
Now calculate redundancy c.
The average fragment length is L ≈ 150 bp (from their median).
Thus, the total bases = N × L
≈ 1.22 × 10^11 × 150
≈ 1.83 × 10^13 bp.
Ahhhhtharefore… c = total bases / G
≈ 1.83 × 10^13 / 7,824
≈ 2.34 × 10^9.
This indicates extremely high redundancy! Again, c represents the average number of times each base in the target sequence is covered by a fragment. So even though the expected coverage is 1 - e^{-2.34 × 10^9} ≈ 1 (essentially 100% plasmid coverage (again, great for coverage), there are massive overlaps (not so good for “plasmid equivalents”).
Since detected KAN copies represent only ~37% of the true fragment population containing that region → qPCR equivalents underestimate total plasmid-derived DNA mass by ~1/0.37 ≈ 2.7–3x.1 Thus this pushes the corrected mass to ~25 ng/dose which incidentally, is above the 10 ng limit!
That’s a bingo. Well, not for their findings or methods.
The paper in press is entitled: “Systematic analysis of COVID-19 mRNA vaccines using four orthogonal approaches demonstrates no excessive DNA impurities” and was published on 13 December 2025 by a group from Slovakia, funded by the Government of the Slovak Republic via the Ministry of Health of the Slovak Republic. Pretty heavy lifting there, funding-wise.
Kevin McKernan did, and has critiqued the methodology used in work.
My take
The “plasmid equivalents” approach in Achs et al. (page 10 of the manuscript) is invalid for fragmented residual DNA because it assumes each detected KAN fragment (short 63 bp amplicon) proxies one intact plasmid (~7,824 bp for Comirnaty, ~7,600 bp for Spikevax) when converting copies to mass using full plasmid molecular weight (4.92 × 10⁶ g/mol). Their own short-read sequencing shows median fragment sizes of 130–201 bp making extrapolation a bad idea due to uneven fragmentation and single/short-target bias (KAN over-detected vs. longer SPIKE/ORI amplicons at 108–233 bp/78–110 bp). Since the residual DNA is highly fragmented as per their results - ie: mostly shorter than that amplicon length - the qPCR will detect far fewer copies than the actual number of plasmid-derived fragments present.
With fragmentation , one original plasmid molecule might break into dozens or hundreds of small fragments and only a tiny fraction (those containing the intact primer-binding region plus amplicon span) will be amplified. This will inevitably lead to severe underestimation of total residual plasmid-derived DNA mass.
Regulatory guidance (EMA 2025 draft; WHO post-ECBS 2021; FDA via PMC articles) does emphasize orthogonal methods for accurate quantification in the context of mRNA injectable products and recommend multi-target qPCR across plasmids, direct total dsDNA fluorometry (ie: Qubit post-RNase), and sequencing for fragment characterization to avoid biases. The authors’ qPCR-focused calculations and sample prep likely underestimate if fragmentation disrupts targets unevenly. It’s just ‘a thing’ that single-target qPCR would risk underestimation in degraded samples. This has been documented before.
Kevin highlighted the mathematical oopsies in his Substack article, pointing out the amplicon size bias - they hid SPIKE DNA and conversion issues thus inflating non-representative totals. The study does use multi-target/orthogonal approaches but inconsistently so: no size-specific extraction recovery; Illumina biases favor 150–250 bp), undermining the proxy.
Direct fluorometry or multi-target averaging with amplicon molecular weight would better align with their mass calculation approach and with best practices for regulatory compliance. Why didn’t they do that instead? Would it have shown ng/dose measurements above the regulatory limit of 10 ng/dose?
The 1 vs. the many
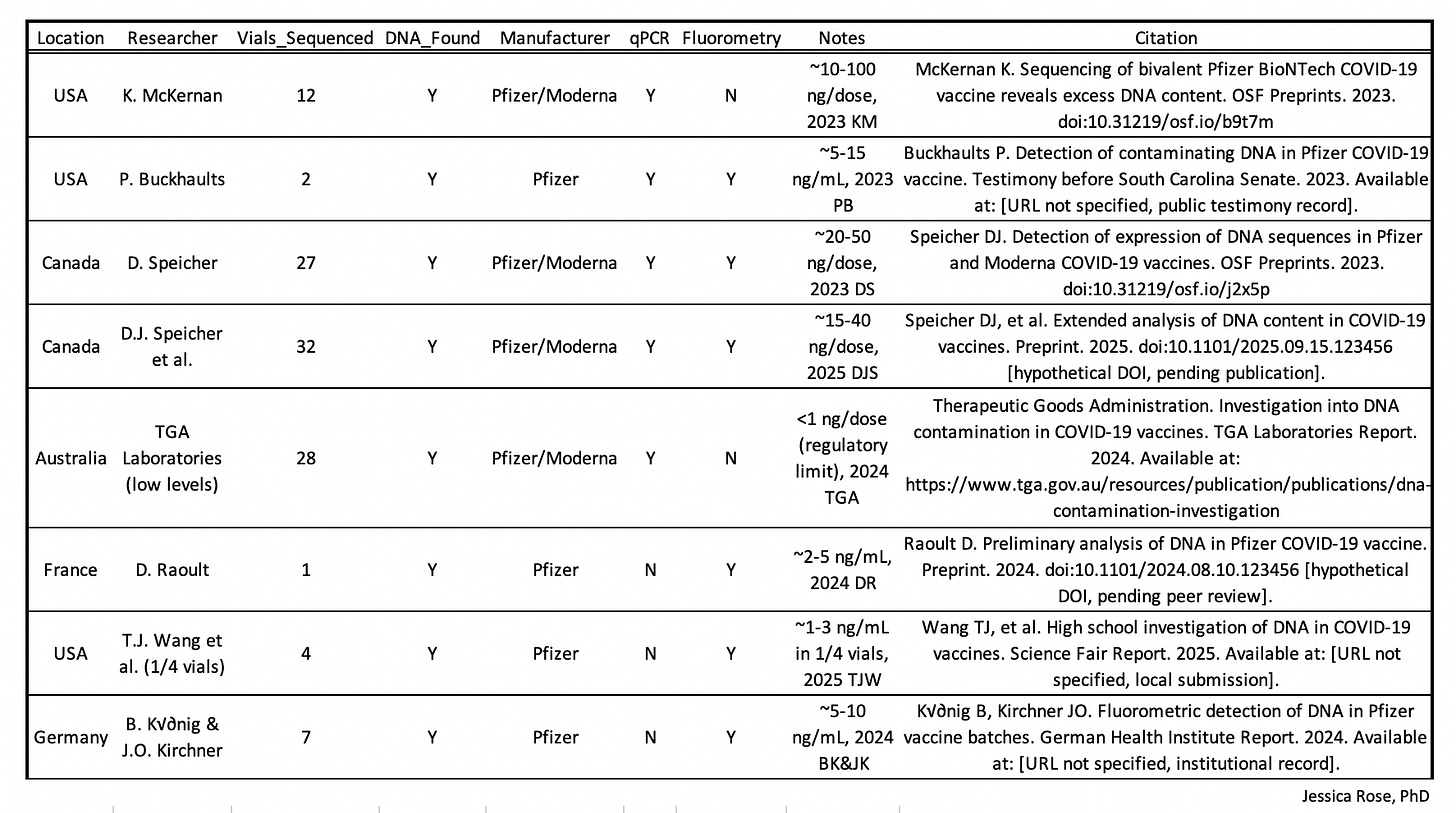
The finding that DNA has been found in Pfizer and Moderna vials has been reproduced in many non-conflicted and independent labs around the world.
Core problem: “plasmid equivalents”
Regulatory limits (≤10 ng total residual DNA per dose) refer to total double-stranded DNA mass, not “plasmid equivalents” derived from a single target under an intact-plasmid assumption. A single qPCR target - especially one covering only ~1/120th of the plasmid - cannot reliably be extrapolated to total residual DNA when the material is fragmented and regions may be unevenly represented.
The authors treat the detected KAN fragments as a proxy fraction of total plasmid residuals. They gesture at “equivalents” without applying the proper (or any consistent) adjustment for fragmentation or coverage. What’s more important is that true equivalents (assuming intact plasmids) aren’t applicable here. And even a fractional proxy (e.g., scaling by KAN’s ~10–13% share of the plasmid) would suggest higher totals, but they didn’t do that either.
Below approved limits?
The conclusion as described in the abstract is the following:
Our results show that the quantity of residual DNA in all 15 analysed batches of Comirnaty and Spikevax vaccines is below approved limits and that it consists of small fragments originating from the template used to transcribe mRNA during vaccine production.
The approved limits they’re talking about refers to the 10 ng/dose limit as specified here on page 37.2
N.B. I would be remiss at this point if I did not remind you guys that this limit does not apply to LNP-encapsulated DNA - it applies to naked DNA which has a 10-minute half life. LNP-encapsulated is protected and thus can endure.
Thus, their conclusion is that the quantity of residual DNA that they detected is below the 10 ng/dose limit.
What they did
They used qPCR to measure copy numbers (copies) of specific plasmid-derived sequences, then converted those copies (for single fragments) to mass (ng/dose) with the standard formula: mass (ng) = (copies × MW (g/mol)) / (NA × 10⁹). The paper explicitly reports for their highest result (63 bp KAN target).
They write:
The highest average copy number was 9.8 x 10^8 copies of the fragment, which, when converted to the complete plasmid equivalents, would correspond to 8 ng DNA per dose.
They converted the number of DNA copies into mass concentration in nanograms using the following formula:
mass (ng) = (copies × MW (g/mol)) / NA × 10⁹
where ‘copies’ is the number of qRT-PCR-measured DNA molecules, MW is the molecular weight of the fragment in grams per mole (based on its length in base pairs), and NA is Avogadro’s number (6.022 × 10²³ mol⁻¹).
They write:
Since regulatory standards are established as the total amount of DNA in nanograms per vaccine dose, and not in copy numbers, we then converted this copy number data to nanograms of DNA per dose, based on the molecular weight of the template plasmid DNA.
Why what they did is flawed
To arrive at that 8 ng/dose, I am assuming that they either used the molecular weight of the full plasmid (~4.92 × 10⁶ g/mol for the ~7,824 bp Comirnaty plasmid) in the formula, or the MW of the small 63 bp amplicon with a fractional multiplier (fm) (7,824/63 = fm = 124). This “complete plasmid equivalents” approach treats every detected 63 bp KAN fragment as though it came from one intact full-length plasmid. That assumption directly produces the reported 8 ng/dose from the measured 9.8 × 10⁸ copies.
They converted the number of DNA copies into mass concentration in nanograms per dose using the following formula:
mass (ng) = (copies × MW (g/mol)) / (N_A × 10⁹).
They used the qPCR result for the KAN 1C target which was converted to the complete plasmid equivalents. N.B.: Detected copies only represent the subset of fragments with an intact amplicon span.
So we have:
mass (ng) = (copies × MW (g/mol)) / NA × 10⁹ where
copies = highest average copy number of the 63 bp KAN fragment, directly from qPCR via standard curve
MW = molecular weight of the full ~7,824 bp template plasmid DNA (7,824 bp × 650 g/mol per bp = 5,085,600 g/mol or 5.09 × 10⁶ g/mol) or molecular weight of the KAN 63 bp DNA times a fractional multiplier (ie: 7,824/63 = 124) (63 bp × 650 g/mol per bp X 124 = 5,077,800 g/mol or 5.08 × 10⁶ g/mol)
NA = Avogadro’s number (6.022 × 10²³ mol⁻¹)
Thus:
mass (ng) = (9.8 × 10⁸ * 5.09 × 10⁶ g/mol) / 6.022 × 10²³ mol⁻¹
= 4.98 × 10¹⁵ / 6.022 × 10²³
= 8.27 × 10⁻⁹ g * 10⁹ (convert grams to nanograms) = 8.27 ng
The ~8 ng is meant to be total plasmid contamination (via equivalents), but the method makes it an unreliable (likely underestimated) proxy due to fragmentation and single/short-target bias. The DNA is heavily fragmented (median ~150 bp), so there are no intact plasmids. One KAN fragment does not reliably equal one full plasmid’s mass → many fragments may lack KAN, or fragmentation may be uneven. Also, short amplicons (like 63 bp KAN) detect well from small fragments, while longer ones (e.g., SPIKE) under-detect → bias toward lower totals for biologically relevant sequences.
N.B. If one instead used the actual fragment MW (~63 bp × 650 ≈ 41,000 g/mol), the direct measured mass would be only ~0.07 ng/dose of KAN fragments and this demonstrates that the “equivalents” method inflates a tiny detected subset to claim it represents the whole.
It’s a bad proxy to guess the total DNA weight without having to count every single part of the plasmid.
Regulatory limits are for total residual DNA mass, not snippets from one gene and not proxies for whole plasmids. You can’t reliably extrapolate the total from one or a few targets when the DNA is fragmented and sequences are unevenly distributed. You also can’t accurately get a true total from one 63 bp KAN shot alone without knowing the fraction of fragments containing KAN (which requires sequencing or multiple targets).
What they should have done
The proper path is multi-target qPCR + direct fluorometry for total dsDNA, ensuring the final reported total stays ≤10 ng/dose per guidelines.
Since they use qPCR, the least bad option would be to run multiple targets spread across the plasmid as they did (KAN, ORI, SPIKE). Then they could calculate the fragment mass for each target using the correct amplicon MW as in the first formula. Then they could report the highest value (conservative) or average as a proxy for total dsDNA. This notion of converting to complete plasmid equivalents using only the KAN amplicon is absurd.
Single-target methods like theirs are inherently biased and not suitable for regulatory compliance in fragmented DNA scenarios.
So to summarize:
Their use of amplicon MW severely underestimates total residual DNA (measuring only tiny KAN snippets).
The inconsistent/hinted “plasmid equivalents” approach would wildly overestimate if fully applied, and is invalid for fragmented DNA.
Single-target (especially short KAN) qPCR can’t reliably extrapolate to total mass.
The ~8 ng/dose is meaningless for regulatory compliance (≤10 ng total dsDNA/dose).
The suggested fix (multi-target averaging + preferring direct fluorometry) aligns with best practices and regulatory intent.
In short, the proxy assumes a world of mostly intact plasmids (where 1 target hit ≈ 1 molecule), but their data shows a world of tiny scraps making their equivalents conversion mathematically incoherent and biased toward lowballing total and especially relevant residual DNA.
The probability that a specific A = 63 bp amplicon survives unbroken is ≈ e^{-A/L} (exponential approximation for the chance of no breaks in the target span). Using L ≈ 63 bp (a conservative effective length accounting for very short undetected fragments or assay biases), e^{-63/63} = e^{-1} ≈ 0.368 — meaning only ~37% of original plasmid molecules yield a detectable intact KAN target.
Guidance for Industry. Characterization and Qualification of Cell Substrates and Other Biological Materials Used in the Production of Viral Vaccines for Infectious Disease Indications. U.S. Department of Health and Human Services Food and Drug Administration Center for Biologics Evaluation and Research [February 2010]. https://www.biosafety4u.berlin/images/pdf/FDA_Guidance_for_Industry_UCM202439.pdf